Empirical Rule Chart
Empirical Rule Chart - Here you will learn how to use the empirical rule to estimate the probability of an event. The 95% rule states that approximately 95% of observations fall within two standard deviations of the mean on a normal distribution. The empirical rule is just a rough estimate of that. Web the empirical rule. 2 solving problems using your curve. Input mean and standard deviation, calculate, and explore the 68%, 95%, and 99.7% intervals. January 3, 2024 fact checked. 95% of data values fall within two standard deviations of the mean. Web the empirical rule is a rule telling us about where an observation lies in a normal distribution. Web in this reading, we will practice applying the empirical rule to estimate the specific probability of occurrence of a sample based on the range of the sample, measured in standard deviations. The rule tells us that, for a normal distribution, there’s a. Web the empirical rule in statistics, also known as the 68 95 99 rule, states that for normal distributions, 68% of observed data points will lie inside one standard deviation of the mean, 95% will fall within two standard deviations, and. Web it can be helpful to write out. 68% of data values fall within one standard deviation of the mean. Web effortlessly analyze data distribution with our empirical rule calculator. The rule states that (approximately): It estimates the proportion of the measurements that lie within one, two, and three standard deviations of the mean. 68% of the observations lie within one standard deviation to either side of the. That is, 68 percent of data is within one standard deviation of the mean; Web the empirical rule is a rule telling us about where an observation lies in a normal distribution. Web the empirical rule. Web when you have normal data, the empirical rule allows you to understand it quickly. Web the empirical rule is a statement about normal. Clear results and an intuitive chart provide instant insights into your dataset's spread. The graphic below is a representation of the empirical rule: Web the empirical rule is a rule telling us about where an observation lies in a normal distribution. 95 percent of data is within two standard deviation of the mean and 99.7 percent of data is within. Web when you have normal data, the empirical rule allows you to understand it quickly. Here you will learn how to use the empirical rule to estimate the probability of an event. Web effortlessly analyze data distribution with our empirical rule calculator. 95% of data values fall within two standard deviations of the mean. Standard deviations of the mean. Your textbook uses an abbreviated form of this, known as the 95% rule, because 95% is the most commonly used interval. 2 solving problems using your curve. 68% of the observations lie within one standard deviation to either side of the mean. The empirical rule states that approximately 68% of data will be within one standard deviation of the mean,. Web the empirical rule is a statistical theory stating that 99.7% of normally distributed data will fall within three standard deviations from the dataset's mean. Input mean and standard deviation, calculate, and explore the 68%, 95%, and 99.7% intervals. 68% of the observations lie within one standard deviation to either side of the mean. Mean (μ or x̄) standard deviation. Web the empirical rule in statistics, also known as the 68 95 99 rule, states that for normal distributions, 68% of observed data points will lie inside one standard deviation of the mean, 95% will fall within two standard deviations, and. Alternatively, you can look up ions in the solubility chart. 95% of data values fall within two standard deviations. Web effortlessly analyze data distribution with our empirical rule calculator. The graphic below is a representation of the empirical rule: 68% of the observations lie within one standard deviation to either side of the mean. 95 percent of data is within two standard deviation of the mean and 99.7 percent of data is within three standard deviation. Standard deviation of. Mean (μ or x̄) standard deviation (σ or s) 68% of the observations lie within one standard deviation to either side of the mean. Web in this reading, we will practice applying the empirical rule to estimate the specific probability of occurrence of a sample based on the range of the sample, measured in standard deviations. 99.7% of data values. The empirical rule states that approximately 68% of data will be within one standard deviation of the mean, about 95% will be within two standard deviations of the mean, and about 99.7% will be within three standard deviations of the mean. The normal curve showing the empirical rule. Why isn't the mean 50%? Here you will learn how to use the empirical rule to estimate the probability of an event. Mean (μ or x̄) standard deviation (σ or s) 68% of the observations lie within one standard deviation to either side of the mean. It estimates the proportion of the measurements that lie within one, two, and three standard deviations of the mean. January 3, 2024 fact checked. Chance a data point falls within ???2??? Web effortlessly analyze data distribution with our empirical rule calculator. Around 68% of values are within 1 standard deviation from the mean. The empirical rule is just a rough estimate of that. 2 solving problems using your curve. Web the empirical rule. The graphic below is a representation of the empirical rule: Clear results and an intuitive chart provide instant insights into your dataset's spread.[Solved] Help with this please Scores of an IQ test have a bellshaped

mechanical engineering Usage of the threesigma limits in calculating
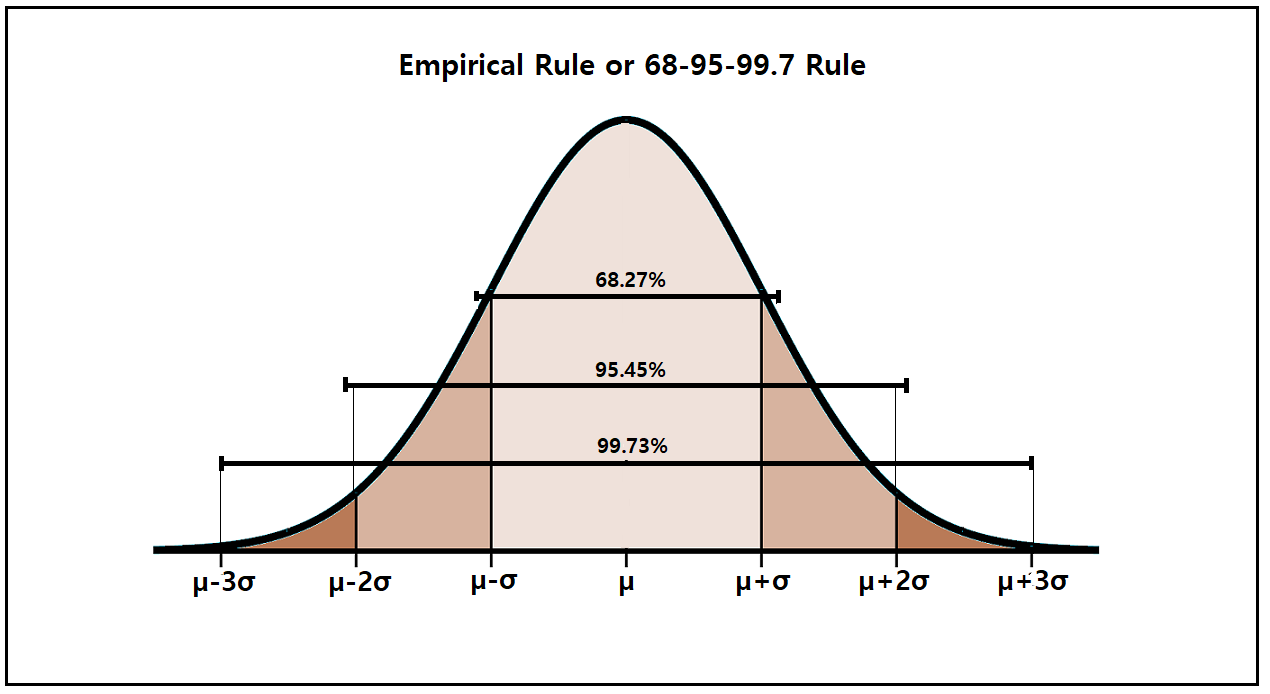
Simplest Explanation of Normal Distribution TheAnalyticsGeek
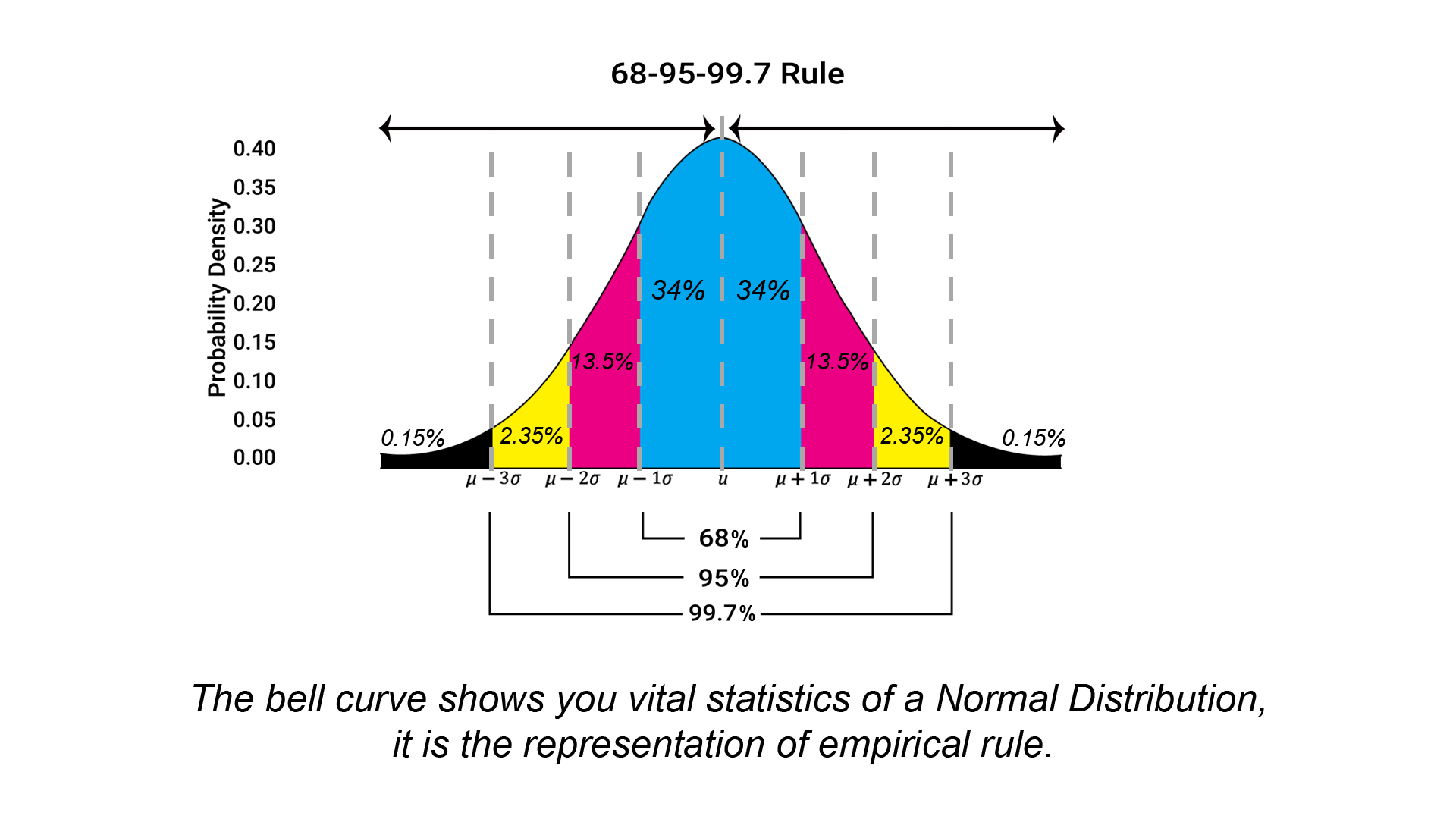
Empirical Rule Calculator
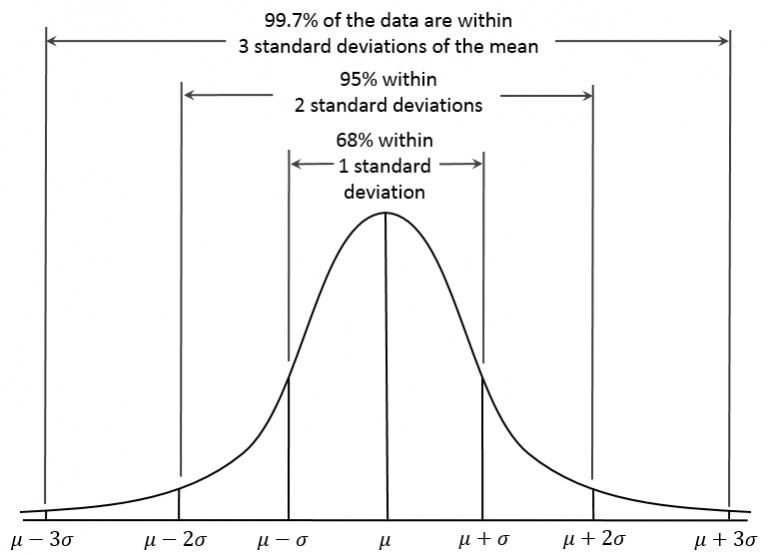
Empirical Rule (Free Stat Lesson) Example Problems
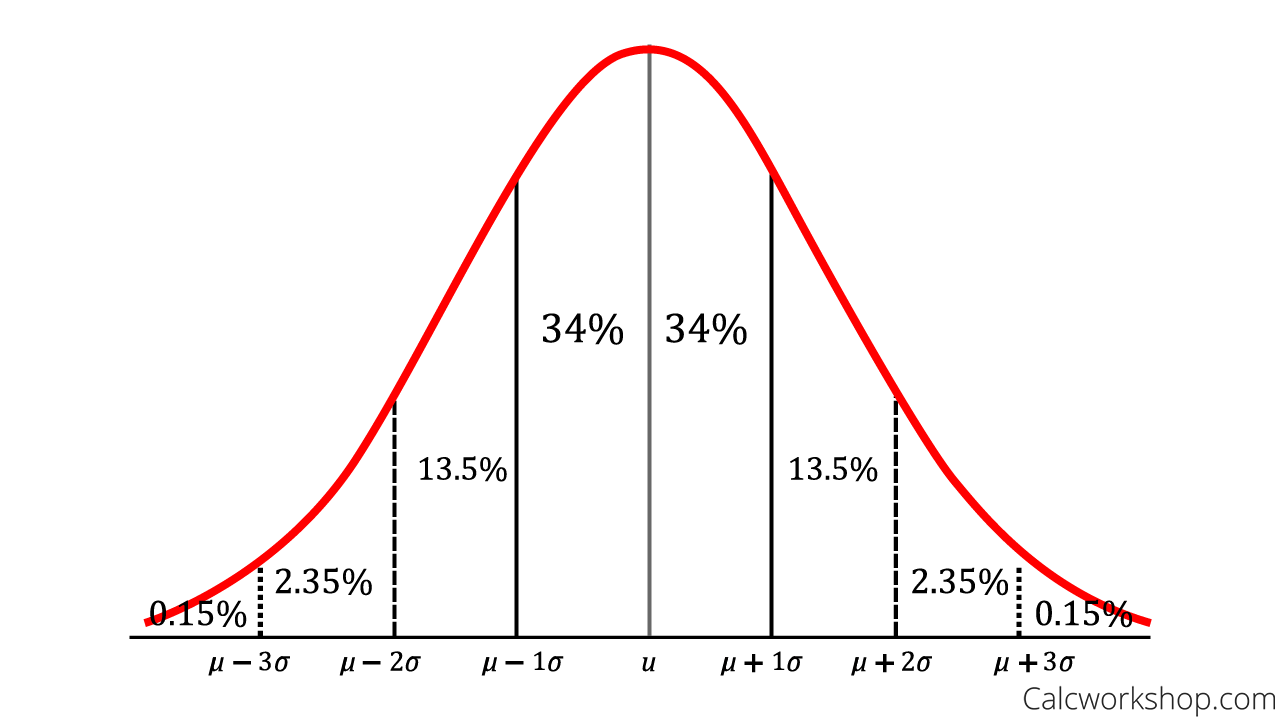
Empirical Rule Problems

38+ empirical rule probability calculator TomaWarner
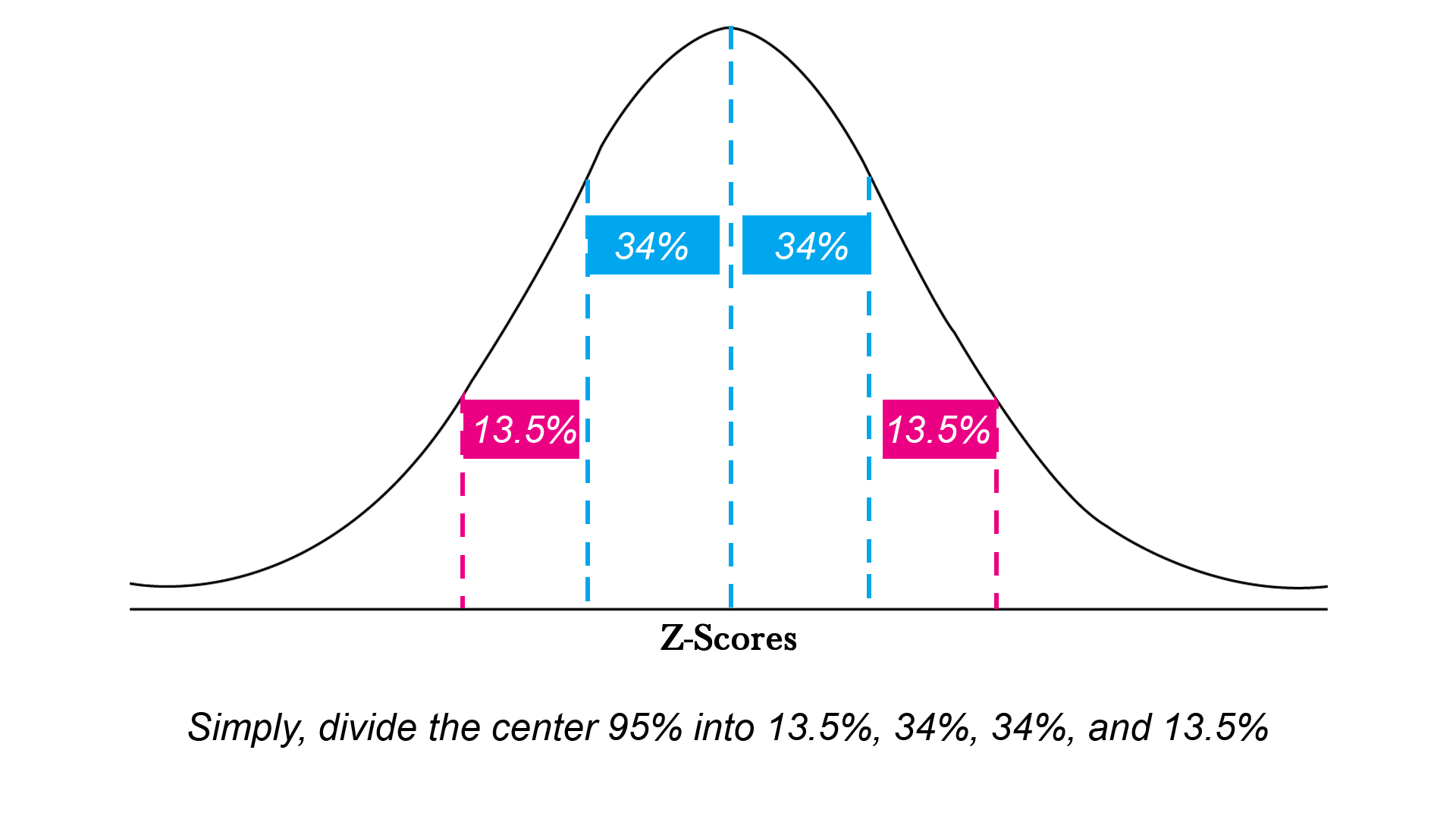
Empirical rule calculator Find Ranges 1, 2, 3 From the Mean
[Solved] The graph illustrates a normal distribution for the prices

Empirical Rule Normal Curve Example 3 YouTube
Web In Mathematics, The Empirical Rule Says That, In A Normal Data Set, Virtually Every Piece Of Data Will Fall Within Three Standard Deviations Of The Mean.
Input Mean And Standard Deviation, Calculate, And Explore The 68%, 95%, And 99.7% Intervals.
The 95% Rule States That Approximately 95% Of Observations Fall Within Two Standard Deviations Of The Mean On A Normal Distribution.
The Rule Tells Us That, For A Normal Distribution, There’s A.
Related Post: